02. Optimal Substructure Property

 http://www.geeksforgeeks.org/dynamic-programming-set-2-optimal-substructure-property/

 Dynamic Programming - Set 2. Optimal Substructure Property

 Set 1에서 설명했 듯, Dynamic Programming으로 풀 수 있는 문제는 다음 두 주요 특성을 가진다.

 1) Overlapping Subproblems
 2) Optimal Substructure

 Set 1에서 이미 Overlapping Subproblem에 대해 설명했으며, 여기서는 Optimal Substructure에 대해 설명한다.

 2) Optimal Substructure: Optimal Substructure의 특징을 가진 문제는 그 subproblem들의 최적화된 솔루션으로 문제의 최적화된 솔루션을 구할 수 있다. 예를 들어 최단경로 문제는 다음과 같은 Optimal Substrucure 특징을 갖는다: 만약 노드 x가 원시노드 u와 목적지노드 v 사이의 최단 경로에 놓여진다면  u에서 v까지의 최단경로는 u에서 x까지의 최단경로와 x에서 v까지의 최단경로의 조합이 될 것이다. 플로이드-워셜 알고리즘과 벨먼-포드 알고리즘같은 일반적인 전체-쌍 최단경로 문제의 알고리즘이 Dynamic Programming의 전형적인 예이다.

 반면에 최장경로 문제는 Optimal Substructure 특징을 갖지 않는다. 다음 그래프의 두 노드간의  최장단순경로를 살펴보자.

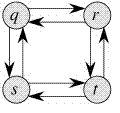
 q에서 t로 가는 두 최장경로가 있다: q -> r ->t 와 q ->s->t. 최단경로와는 다르게, 이 최장경로들은 Optimal Substructure 특징을 갖지 않는다. 예를 들어, 최장경로 q->r->t은 q에서 r, r에서 t까지의 최장경로들의 조합이 아니다. 왜냐하면 q에서 r까지의 최장경로는 q->s->t->r이기 때문이다.